GGX+Smith 微表面 PBR 漫反射光照

原标题

PBR Diffuse Lighting for GGX+Smith Microsurfaces

通用的微表面 BRDF

通用形式

宏观表面的 BRDF 只是许多微表面的平均。

  • 通用形式
    ∫Ωρm(L,V,m)D(m)G2(L,V,m)m⋅L∣N⋅L∣m⋅V∣N⋅V∣dm\int_\Omega\rho_m(L,V,m)D(m)G_2(L,V,m)\frac{m\cdot L}{|N\cdot L|}\frac{m\cdot V}{|N\cdot V|}dm

  • ∫Ωdm\int_\Omega dm
    对半球面上所有微表面法线积分。

  • ρm(L,V,m)\rho_m(L,V,m)
    单个微表面如何响应，即法线方向的 BRDF，通常为理想镜面或理想漫反射。

  • D(m)D(m)
    法线分布概率密度函数。

  • G2(L,V,m)G_2(L,V,m)
    微表面 m 同时看到光源和观察者的概率。

  • D(m)G2(L,V,m)D(m)G_2(L,V,m)
    同时被光源和观察者可见的表面的概率密度函数。
    G2G_2 由两个方向（光源、观察者）的可视性 G1G_1 推出。

  • ⟨m⋅L⟩∣N⋅L∣⟨m⋅V⟩∣N⋅V∣\frac{\lang m\cdot L\rang}{|N\cdot L|}\frac{\lang m\cdot V\rang}{|N\cdot V|}
    表面对光源来说有多大，表面对观察者来说有多大。

  • D(m)G2(L,V,m)⟨m⋅L⟩∣N⋅L∣⟨m⋅V⟩∣N⋅V∣D(m)G_2(L,V,m)\frac{\lang m\cdot L\rang}{|N\cdot L|}\frac{\lang m\cdot V\rang}{|N\cdot V|}
    从 L 出发，经过单次反射，到达 V 的概率密度函数。
    ∫ΩD(m)G2(L,V,m)⟨m⋅L⟩∣N⋅L∣⟨m⋅V⟩∣N⋅V∣dm≤1\int_\Omega D(m)G_2(L,V,m)\frac{\lang m\cdot L\rang}{|N\cdot L|}\frac{\lang m\cdot V\rang}{|N\cdot V|}dm\leq 1

如何获得 specular

  • 微表面 BRDF 是完美镜面

  • 光线只在 m = H，的情况下反射

  • 在数学上，BRDF 是经过缩放的狄拉克函数δm(H,m)\delta_m(H,m)

  • 一般情况：
    ∫Ωρ(L,V,N)cosΘVdV=1\int_\Omega\rho(L,V,N)cos\Theta_VdV=1

  • 更改积分域以计算 δ\delta：
    ∫Ωkδm(H,m)cosΘVdVdmdm=1\int_\Omega k\delta_m(H,m)cos\Theta_V\frac{dV}{dm}dm=1

  • kδm(H,m)k\delta_m(H,m) 是纯镜面 BRDF

  • k 是缩放参数

  • dVdm\frac{dV}{dm} 是 V 相对于 m 的变化速度

就结论而言，dVdm=4H⋅V\frac{dV}{dm}=4H\cdot V
这是通过将 dv 从单位球投影至半径为 |L + V| 的球面上得到的。
dVdm

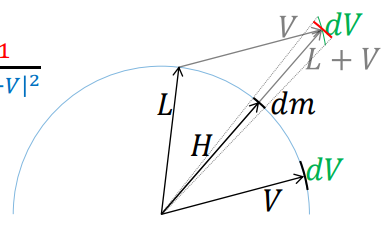
由于 m = H 以及 H⋅V=H⋅LH\cdot V=H\cdot L

  • ∫Ωkδm(H,m)cosΘVdVdmdm=1\int_\Omega k\delta_m(H,m)cos\Theta_V\frac{dV}{dm}dm=1
  • ∫Ωkδm(H,m)(m⋅V)(4H⋅V)dm=1\int_\Omega k\delta_m(H,m)(m\cdot V)(4H\cdot V)dm=1
  • k=14(H⋅L)(H⋅V)k=\frac{1}{4(H\cdot L)(H\cdot V)}

狄拉克函数在其定义域上的积分为 1
为什么 (m⋅V)(H⋅V)(m\cdot V)(H\cdot V) 要以 (H⋅L)(H⋅V)(H\cdot L)(H\cdot V) 的形式保留下来？

  • 故，完美镜面 BRDF：
    δm(H,m)4(H⋅L)(H⋅V)\frac{\delta_m(H,m)}{4(H\cdot L)(H\cdot V)}

  • 加上菲涅尔项
    ρm(L,Vm)=F(L,m)δH(m)4∣H⋅L∣∣H⋅V∣\rho_m(L,Vm)=F(L,m)\frac{\delta_H(m)}{4|H\cdot L||H\cdot V|}

  • 整合
    ∫Ωρm(L,V,m)D(m)G2(L,V,m)⟨m⋅L⟩∣N⋅L∣⟨m⋅V⟩∣N⋅V∣dm\int_\Omega\rho_m(L,V,m)D(m)G_2(L,V,m)\frac{\lang m\cdot L\rang}{|N\cdot L|}\frac{\lang m\cdot V\rang}{|N\cdot V|}dm

  • 代入得：
    ∫ΩF(L,m)δm(H,m)4∣H⋅L∣∣H⋅V∣D(m)G2(L,V,m)⟨m⋅L⟩∣N⋅L∣⟨m⋅V⟩∣N⋅V∣dm\int_\Omega\frac{F(L,m)\delta_m(H,m)}{4|H\cdot L||H\cdot V|}D(m)G_2(L,V,m)\frac{\lang m\cdot L\rang}{|N\cdot L|}\frac{\lang m\cdot V\rang}{|N\cdot V|}dm

  • 由于狄拉克函数在积分中被消掉，以及 m = H 得：
    Specular BRDF = F(L,H)D(H)G2(L,V,H)4∣H⋅L∣∣H⋅V∣\frac{F(L,H)D(H)G_2(L,V,H)}{4|H\cdot L||H\cdot V|}

扩展至 diffuse

  • 兰伯特漫反射：
    ρm(L,V,m)=1π\rho_m(L,V,m)=\frac{1}{\pi}
  • 无闭合解。
    闭合指的是一个表达式包含有限个标准运算，极限、差分、积分都不算标准运算。

GGX+Smith 微表面模型的漫反射模拟

Shadowing / masking 函数

不相关 vs 高度相关的 G

G2(L,V,m)=G1(L,m)G1(V,m)G_2(L,V,m)=G_1(L,m)G_1(V,m)
不太现实，但是在实践中的效果很好。

Higher points more likely visible to both 𝐿 and 𝑉 (and lower points less likely)

  • 高度不相关的 G 会使镜面反射变暗

    • 越粗糙误差越大
    • 越接近掠射角误差越大

  • 角度相关性

    • 当 L = V，应有 G2(V,V,m)=G1(V,m)G_2(V,V,m)=G_1(V,m)
    • 不相关：G2(V,V,m)=G1(V,m)2G_2(V,V,m)=G_1(V,m)^2
    • 相关：G2G_2 介于两者之间

Smith shadowing / masking

  • 前面没看懂，中间没看懂，但是：

  • Λ(V)=12(α2+(1−α2)(N⋅V)2N⋅V−1)\Lambda(V)=\frac{1}{2}(\frac{\sqrt{\alpha^2+(1-\alpha^2)(N\cdot V)^2}}{N\cdot V}-1)

  • G1(V)=11+Λ(V)G_1(V)=\frac{1}{1+\Lambda(V)}

  • G2(L,V)=11+Λ(L)+Λ(V)G_2(L,V)=\frac{1}{1+\Lambda(L)+\Lambda(V)}

  • G1(L)G1(V)=11+Λ(L)+Λ(V)+Λ(L)Λ(V)G_1(L)G_1(V)=\frac{1}{1+\Lambda(L)+\Lambda(V)+\Lambda(L)\Lambda(V)}

  • G1(V)=G_1(V)=
    2N⋅Vα2+(1−α2)(N⋅V)2+N⋅V\frac{2N\cdot V}{\sqrt{\alpha^2+(1-\alpha^2)(N\cdot V)^2}+N\cdot V}

  • G2(L,V)=G_2(L,V)=
    2(N⋅L)(N⋅V)N⋅Vα2+(1−α2)(N⋅L)2+N⋅Lα2+(1−α2)(N⋅V)2\frac{2(N\cdot L)(N\cdot V)}{N\cdot V\sqrt{\alpha^2+(1-\alpha^2)(N\cdot L)^2}+N\cdot L\sqrt{\alpha^2+(1-\alpha^2)(N\cdot V)^2}}

新的 Smith + GGX G2G_2 近似

  • G1G_1 的分母
    • α2+(1−α2)(N⋅V)2+N⋅V\sqrt{\alpha^2+(1-\alpha^2)(N\cdot V)^2}+N\cdot V
    • lerp((N⋅V)2,1,α2)+N⋅V\sqrt{lerp((N\cdot V)^2,1,\alpha^2)}+N\cdot V
    • 近似：
    • lerp((N⋅V)2,1,α2)≈lerp(N⋅V,1,α)\sqrt{lerp((N\cdot V)^2,1,\alpha^2)}\approx lerp(N\cdot V,1,\alpha)
  • 故，G1(V)≈2N⋅VN⋅V(2−α)+αG_1(V)\approx\frac{2N\cdot V}{N\cdot V(2-\alpha)+\alpha}
    • 和 Unreal 一致：
    • G1(V)≈N⋅VN⋅V(1−k)+kG_1(V)\approx\frac{N\cdot V}{N\cdot V(1-k)+k}, k=α2k=\frac{\alpha}{2}
  • 通过近似的 G1G_1 近似来求得 G2G_2
    • G2(L,V)=2∣N⋅L∣∣N⋅V∣lerp(2∣N⋅L∣∣N⋅V∣,∣N⋅L∣+∣N⋅V∣,α)G_2(L,V)=\frac{2|N\cdot L||N\cdot V|}{lerp(2|N\cdot L||N\cdot V|,|N\cdot L|+|N\cdot V|,\alpha)}
    • 代入 BRDF，约分：
    • BRDF=F(L,H)D(H)2lerp(2∣N⋅L∣∣N⋅V∣,∣N⋅L∣+∣N⋅V∣,α)BRDF=\frac{F(L,H)D(H)}{2lerp(2|N\cdot L||N\cdot V|,|N\cdot L|+|N\cdot V|,\alpha)}
  • 开销：
    • G1(L)G1(V)G_1(L)G_1(V)：F(L,H)D(H)(∣N⋅L∣(2−α)+α)(∣N⋅V∣(2−α)+α)\frac{F(L,H)D(H)}{(|N\cdot L|(2-\alpha)+\alpha)(|N\cdot V|(2-\alpha)+\alpha)}（~4 cycles）
    • G2(L,V)G_2(L,V)：~6 cycles
    • 高度相关产生的额外成本可以忽略不计。
  • 质量：
    • 在粗糙材质的掠射角上效果更好。
    • 高度相关近似 VS 不相关近似
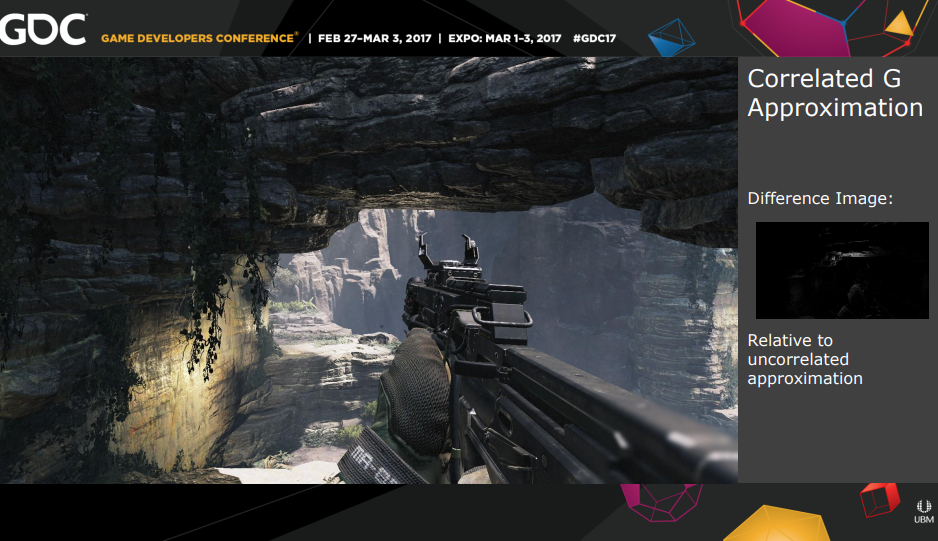
    • 高度相关准确 VS 高度相关近似
    • 感觉是否相关带来的差异比是否准确要大一些。

路径追踪

讨论了一些光追中，BRDF 中菲涅尔项对漫反射以及高光部分的权重问题，先略过。