GAMES101 拾遗

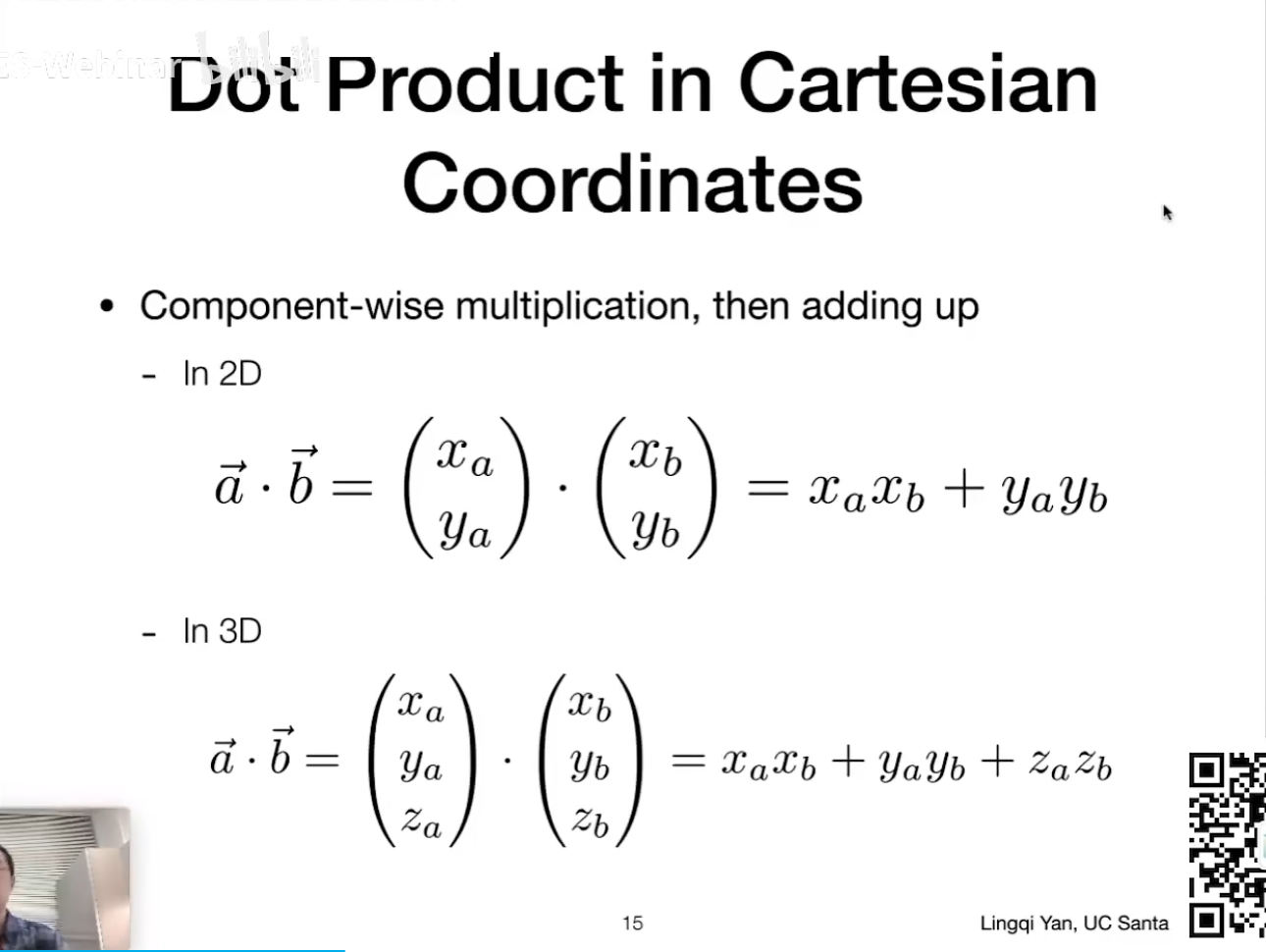
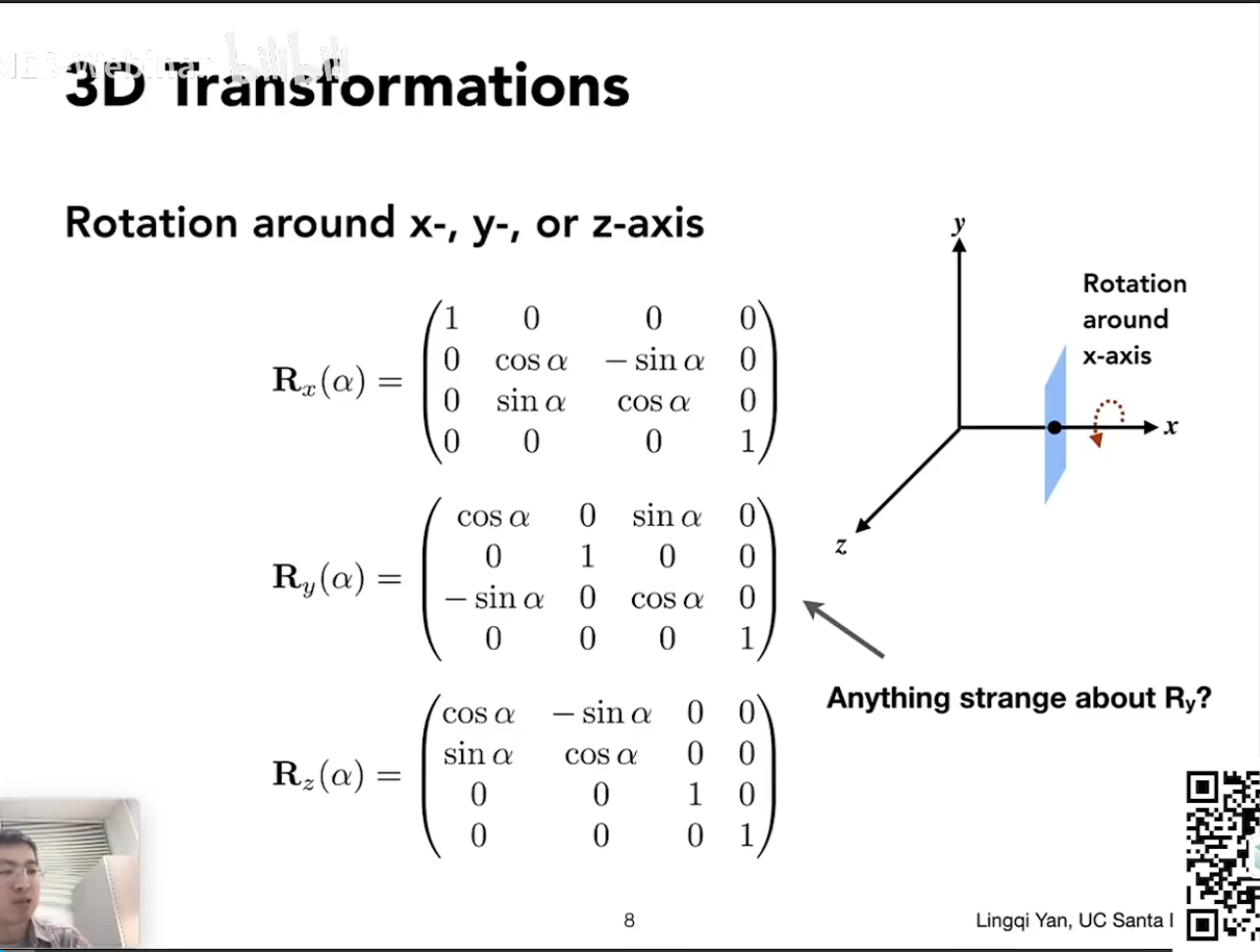
Lecture 02 Review of Linear Algebra

点乘
叉乘

对于一个 vec4，一般认为 w 分量为 1 时表示点，w 分量 为 0 时表示向量。
也符合“点 - 点 = 向量”

Lecture 04 Transformation Cont.

旋转

绕轴旋转
绕任意轴旋转

相机定义

  • 位置：e
  • 看向：g
  • 头顶：t

Frustum 定义

  • tanfovY2=t∣n∣tan\frac{fovY}{2} = \frac{t}{|n|}
  • aspect=rtaspect = \frac{r}{t}

View 矩阵

将相机变换至“位于原点，看向 -Z，头顶为 +Y”
先移动至原点，再旋转
Mview=RviewTviewM_{view}=R_{view}T_{view}

Tview=T_{view}=

(100−xe010−ye001−ze0001) \begin{pmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

由 Rview−1=R_{view}^{-1}=

(xg×txtx−g0yg×tyty−g0zg×tztz−g00001) \begin{pmatrix} x_{g \times t} & x_t & x_{-g} & 0 \\ y_{g \times t} & y_t & y_{-g} & 0 \\ z_{g \times t} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

得 Rview=R_{view}=

(xg×tyg×tzg×t0xtytzt0x−gy−gz−g00001) \begin{pmatrix} x_{g \times t} & y_{g \times t} & z_{g \times t} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Projection 矩阵

先透视，再正交（Frustum -> 长方体 -> 正方体）
MProjection=MOrthographicMPersprctiveToOrthographicM_{Projection}=M_{Orthographic}M_{PersprctiveToOrthographic}

Mp2o=M_{p2o}=

(n0000n0000n+f−nf0010) \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}

MOrthographic=MrotateMtransM_{Orthographic}=M_{rotate}M_{trans}

Mtrans=M_{trans}=

(100−r+l2010−t+b2001−n+f20001) \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Mrotate=M_{rotate}=

(2r−l00002t−b00002n−f00001) \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Viewport 视口变换

Mviewport=M_{viewport}=

(width200width20height20height200100001) \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

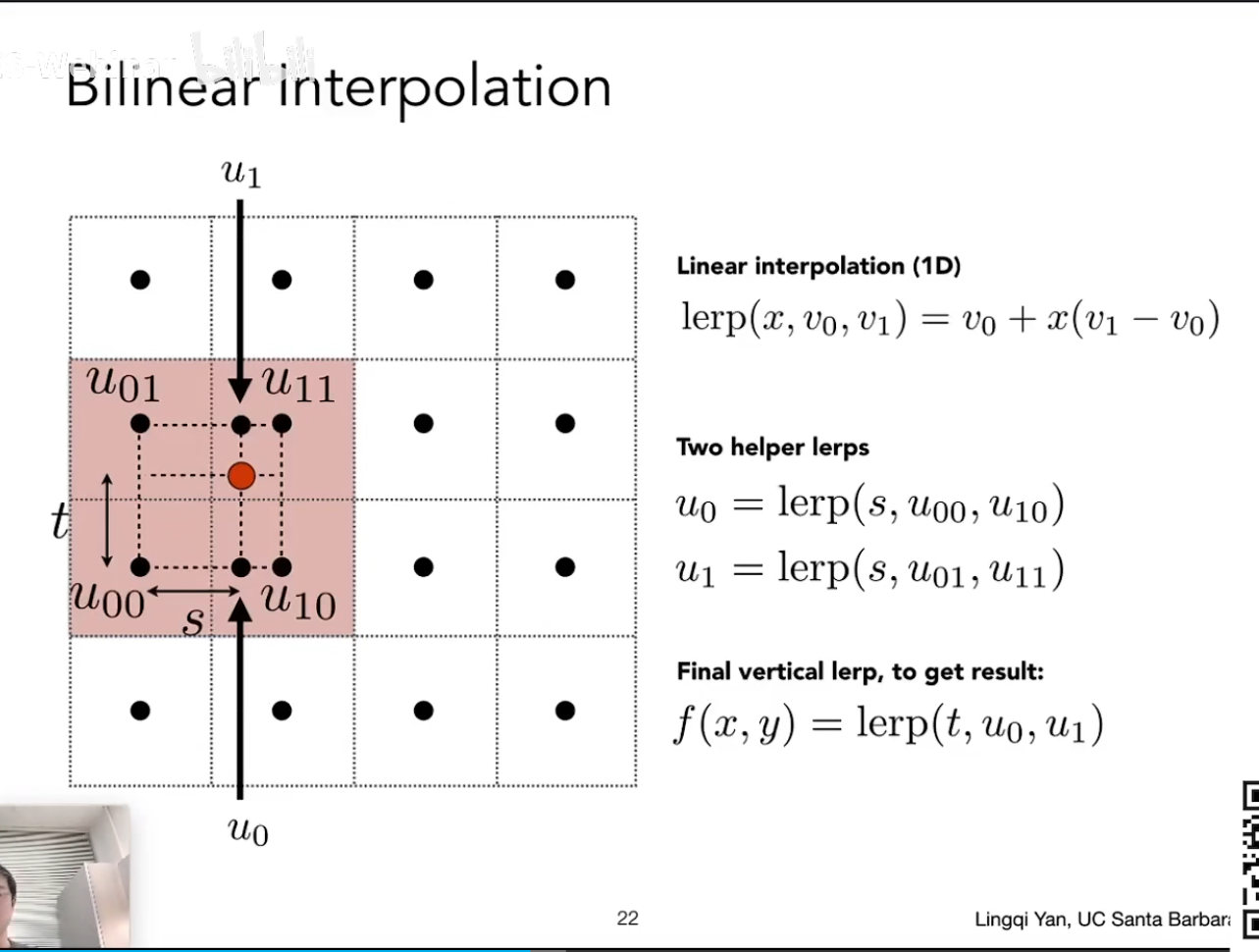
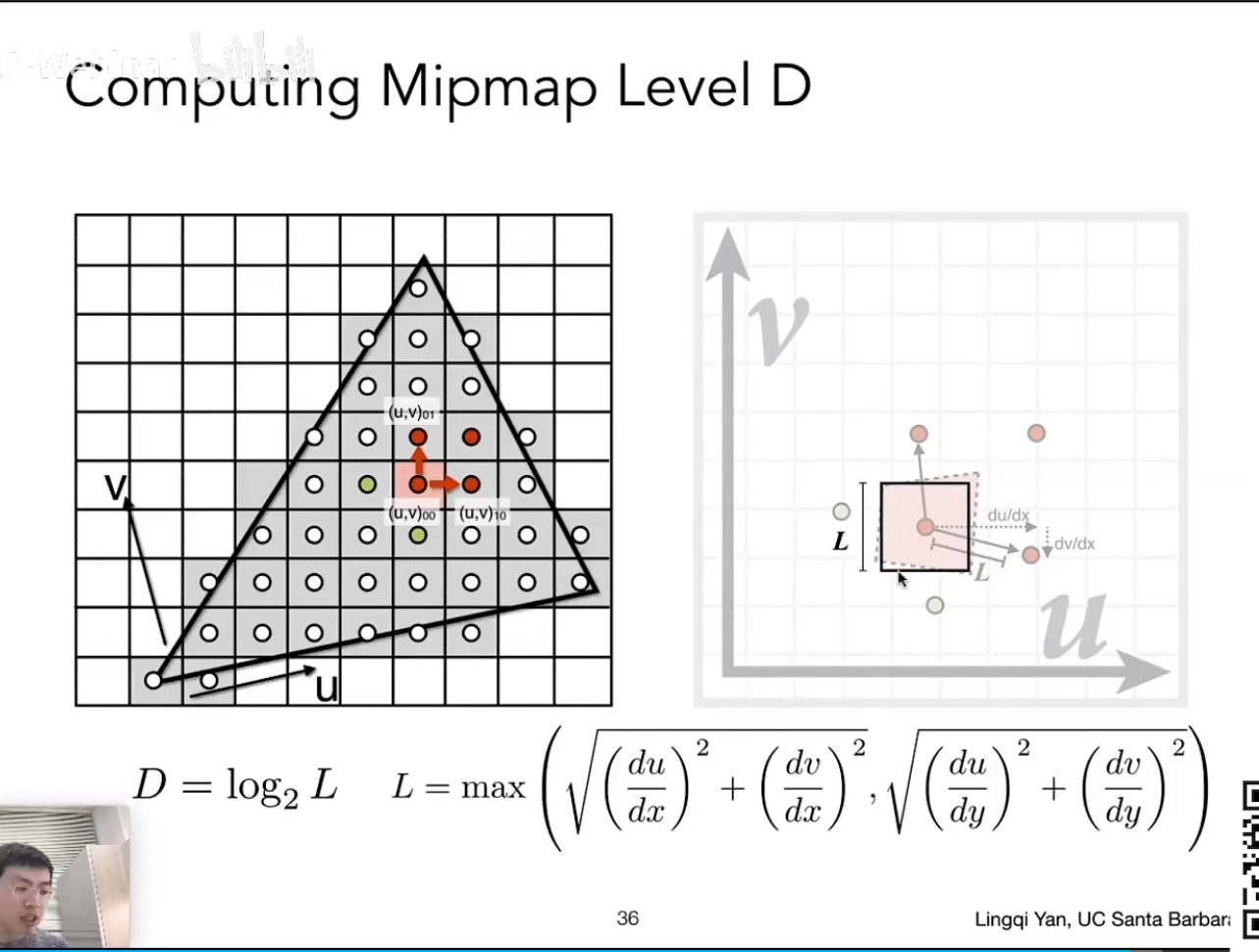
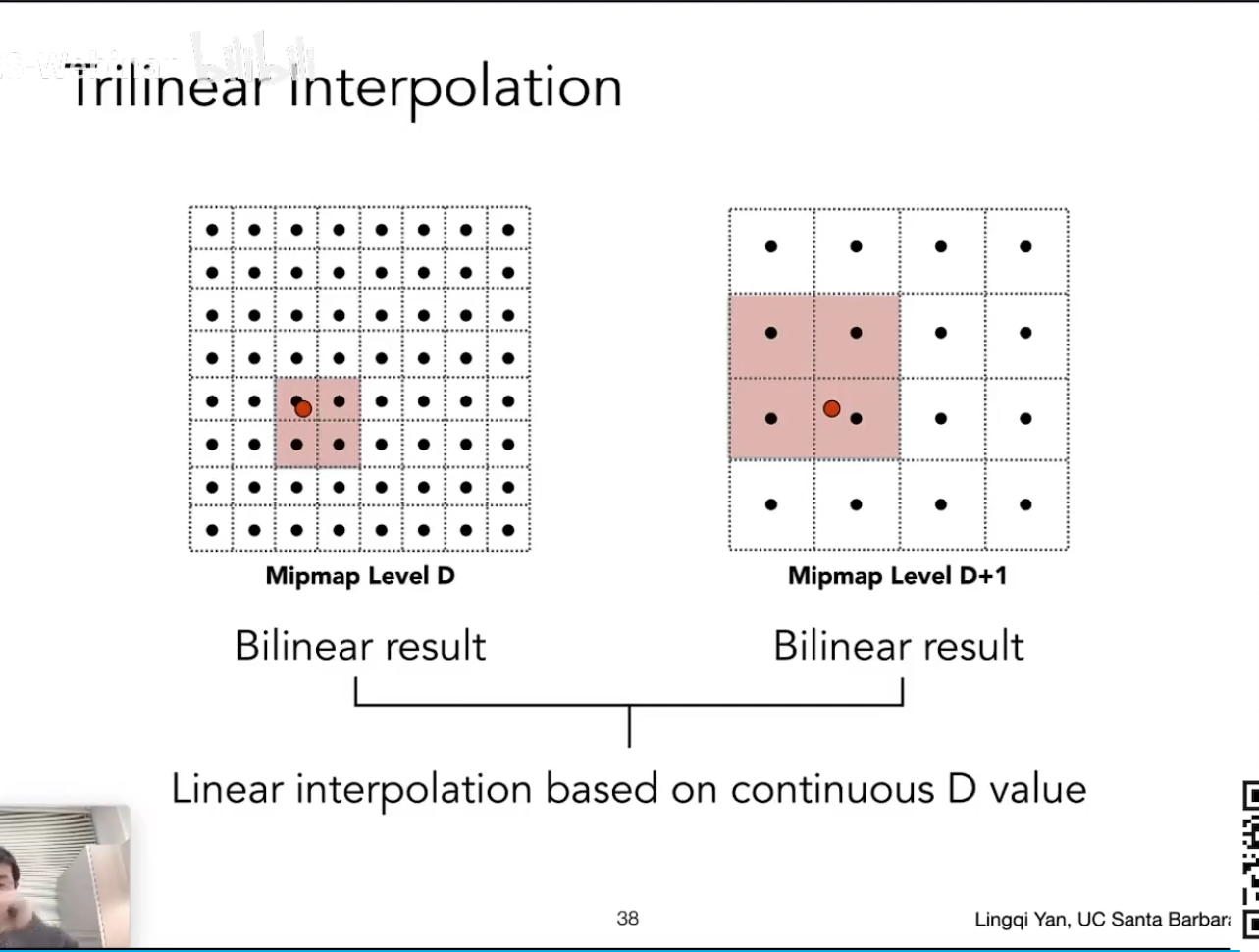
Lecture 09 Shading 3(Texture Mapping Cont.)

重心坐标
重心坐标
双线性插值
Mipmap
三线性插值
Bump

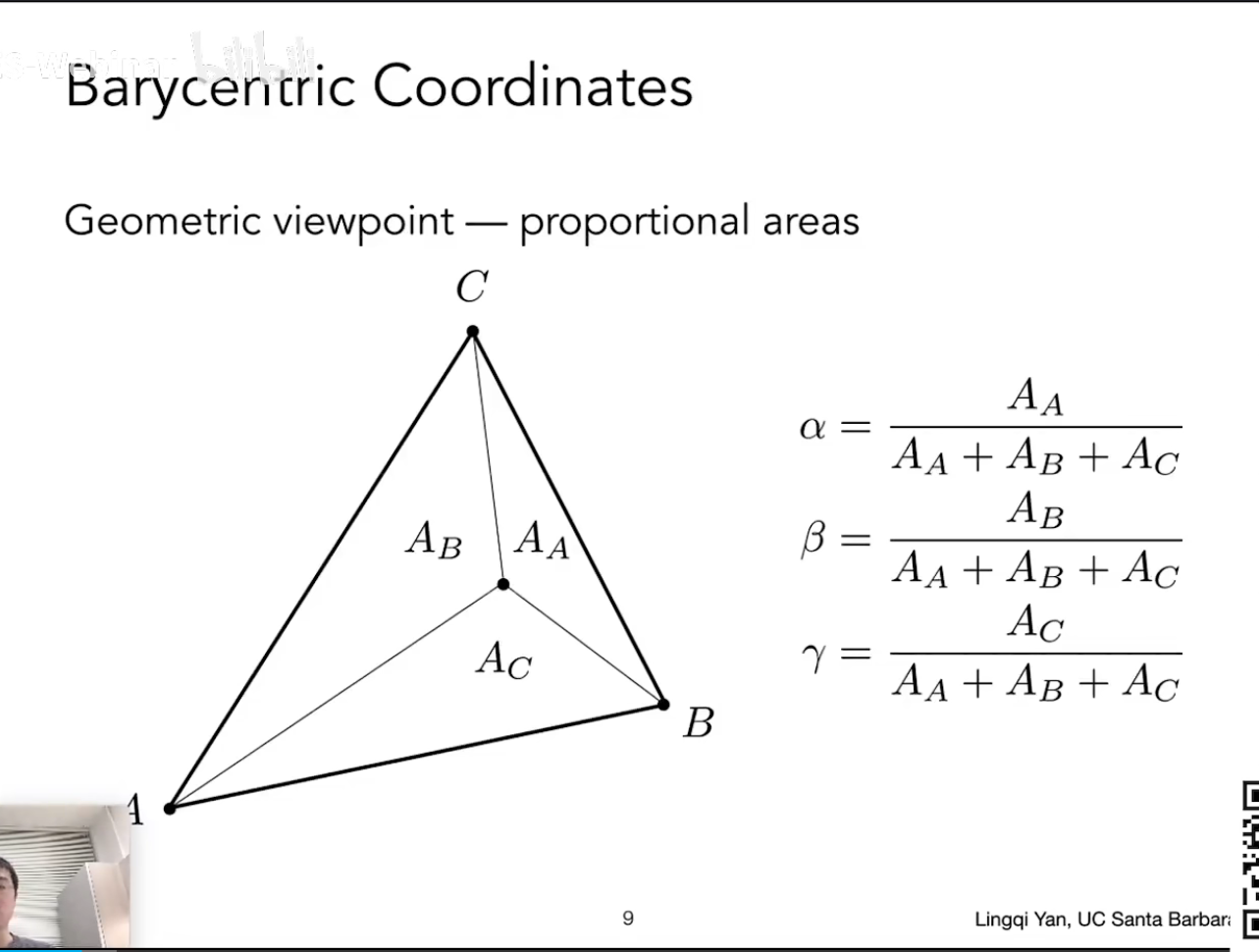
当重心坐标相加为 1 且全部在 [0, 1] 的范围内，即代表点在三角形内。

Lecture 13 Ray Tracing 1

射线平面相交
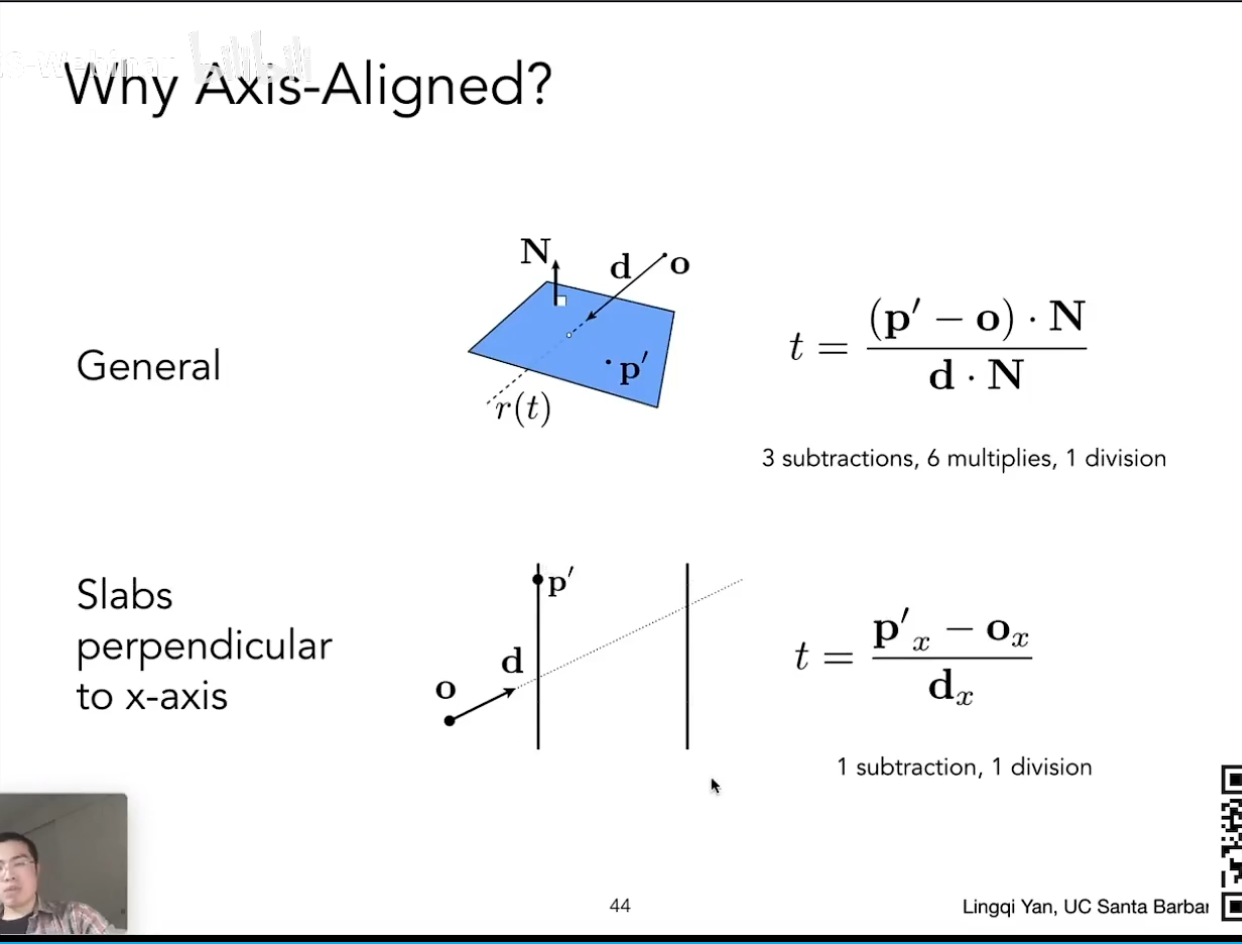
轴对齐的简化
Moller Trumbore 算法

求射线与 AABB 求交

  • 对三个轴每一对平面，计算 tmint_{min} 与 tmaxt_{max}，负值也 OK。
  • 对于 AABB，tenter=max(tmin)t_{enter} = max(t_{min})，texit=min(tmax)t_{exit} = min(t_{max})。
  • 当且仅当 tenter<texitt_{enter} < t_{exit} && texit>=0t_{exit} >= 0 时射线与 AABB 相交。

Lecture 15 Ray Tracing 3

辐射度量学基础

Lecture 16 Ray Tracing 4

蒙特卡洛积分

Lo(p,ωo)L_o(p,\omega_o)

=∫H2Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)dωi=\int_{H^2}L_i(p, \omega_i)f_r(p, \omega_i, \omega_o)(n\cdot \omega_i)d\omega_i

≈1N∑i=1NLi(p,ωi)fr(p,ωi,ωo)(n⋅ωi)p(ωi)\approx\frac{1}{N}\sum^N_{i=1}\frac{L_i(p, \omega_i)f_r(p, \omega_i, \omega_o)(n\cdot \omega_i)}{p(\omega_i)}

Light Sampling

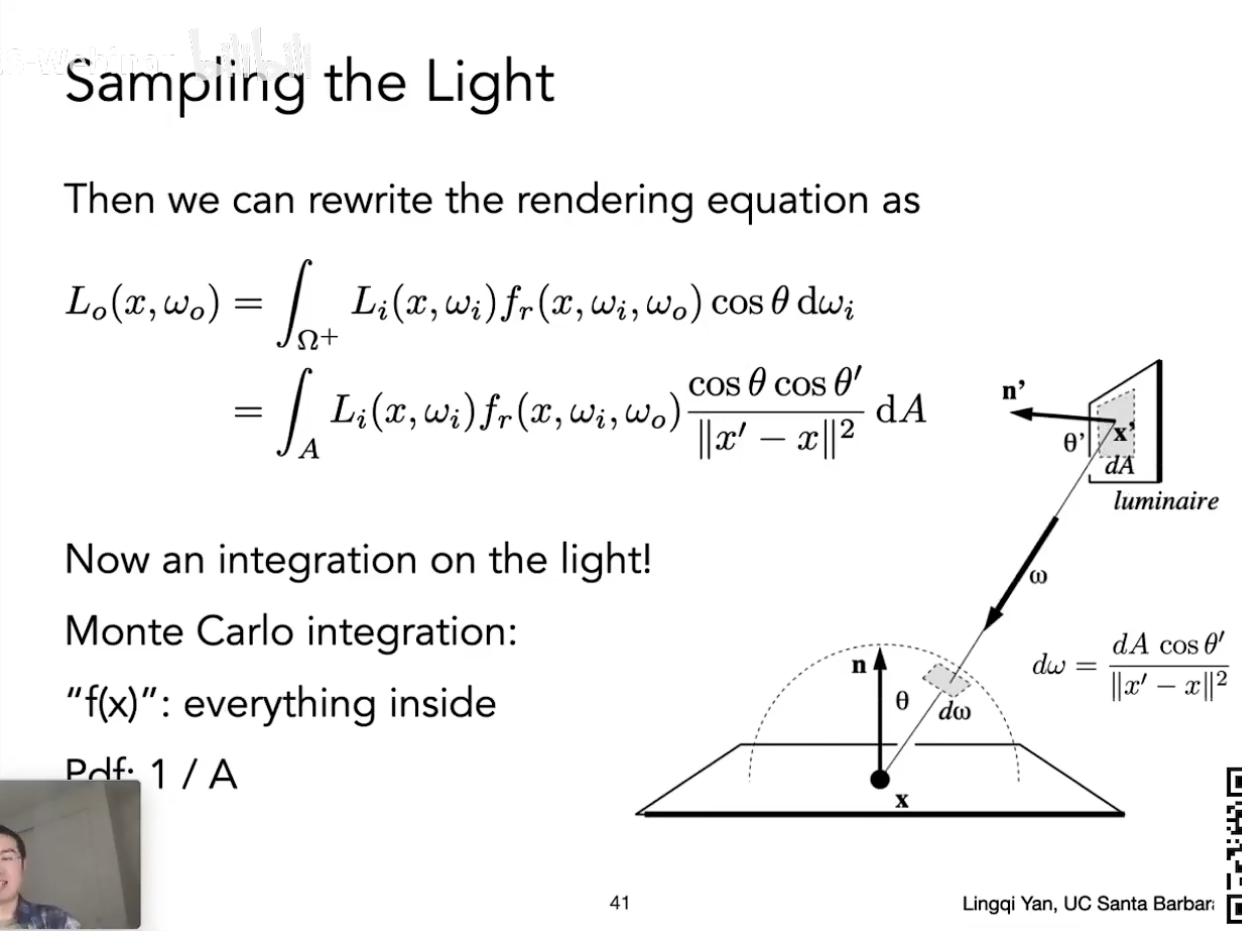
LightSampling

Path Tracing

1
2
3
4
5
6
7
8
9
10
11
12
13
14
shade(p, wo)
  // 来自光源的贡献
  均匀地采样 x' 处的光源（pdf_light = 1 / A）
  如果 p 点和 x' 点之间没有遮挡
    L_dir = L_i * f_r * cosθ * cosθ' / |x' - p|^2 / pdf_light

  // 来自其他表面的贡献
  如果通过以概率 P_RR 进行的轮盘赌测试
    均匀地采样半球（pdf_hemi = 1 / 2pi）
    追踪光线 r(p, wi)
    如果在 q 点击中非光源表面
      L_indir = shade(q, -wi) * f_r * cosθ / pdf_hemi / P_RR

  return L_dir + L_indir

Lambertian 表面的的 BRDF

Lambertian

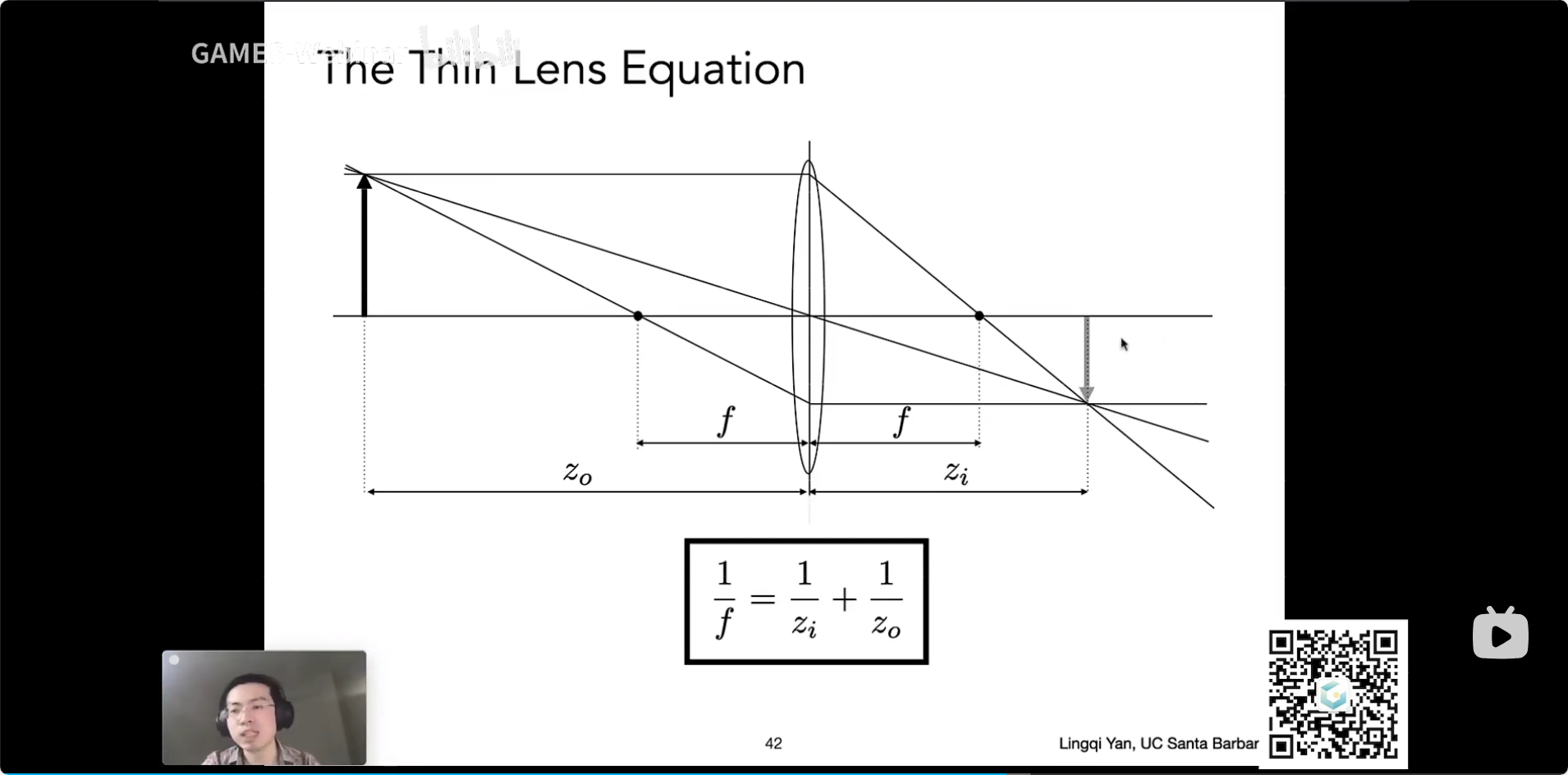
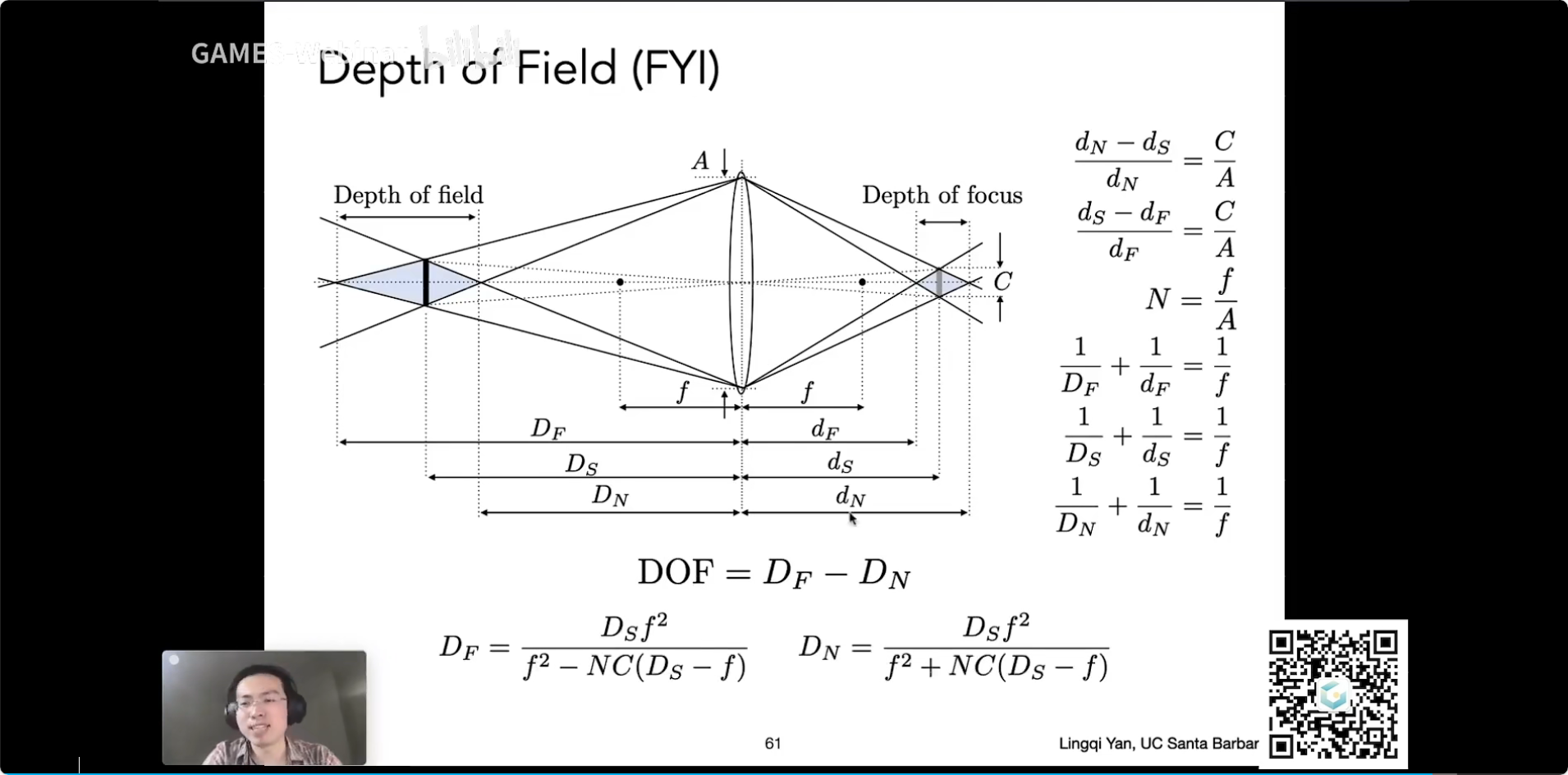
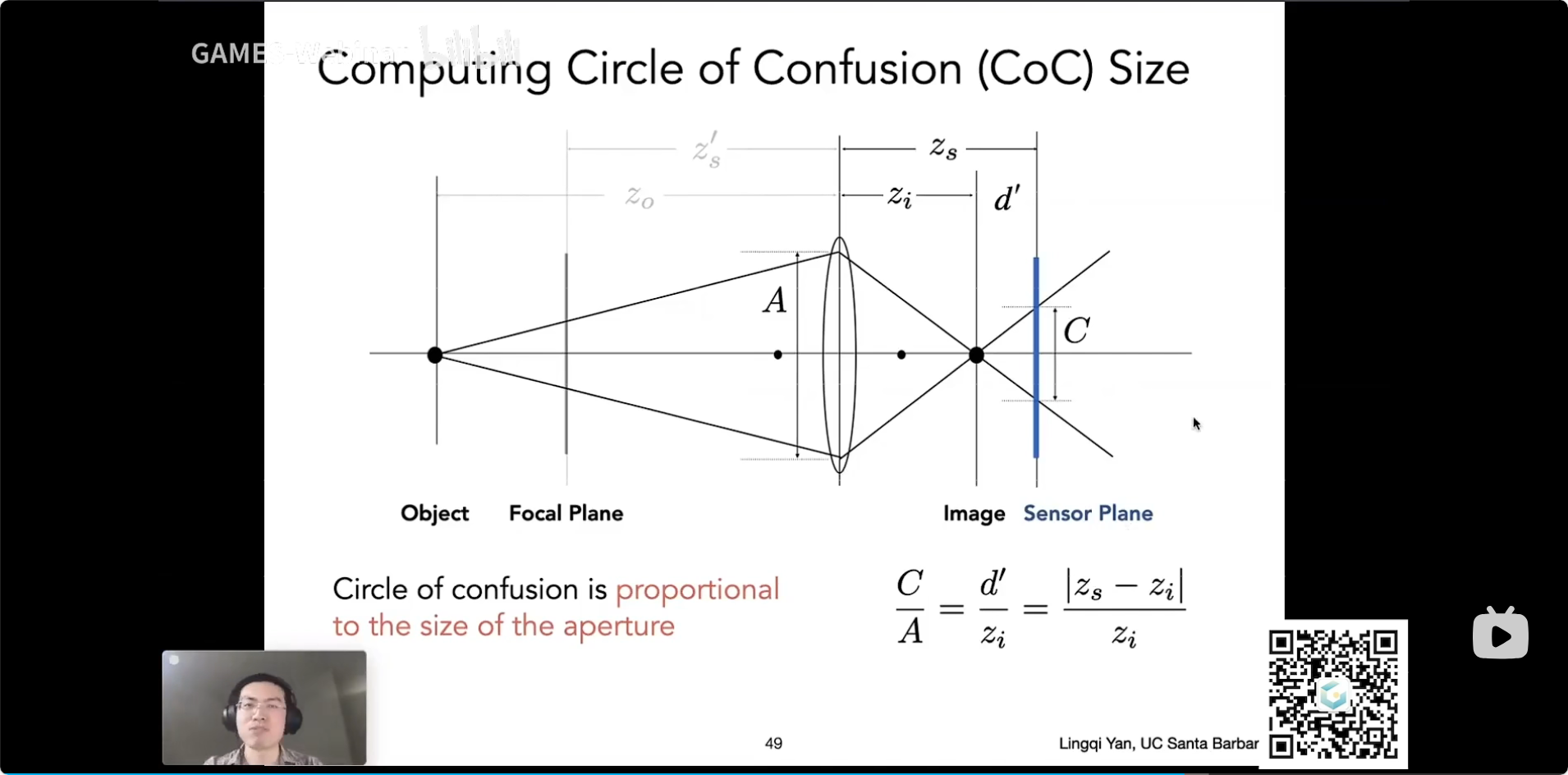
Lecture 19 Cameras, Lenses and Light Fields

Gaussian

Coc
Coc2

DoF