本文最后更新于 2025-03-09T19:33:34+08:00
序言
路径追踪的前置知识。
物理量一览
| 符号 |
名称 |
单位 |
光度学名称 |
光度学单位 |
| Q |
Radiant Energy |
J |
Luminous Energy |
lm.s |
| Φ |
Radiant Flux |
sJ / Watt(W) |
Luminous Flux |
Lumen(lm) |
| I |
Radiant Intensity |
srW |
Luminous Intensity |
Candela(cd) |
| E |
Irradiance |
m2W |
Illuminance |
Lux(lx) |
| L |
Radiance |
m2⋅srW |
Luminance |
Nit(nt) |
Radiant Energy
辐射能量。
Radiant Flux
- Φ=dtdQ (W)
辐射通量,单位时间上的能量。
Radiant Intensity
- I(ω)=dωdΦ (srW)
辐射强度,功率每立体角。
立体角
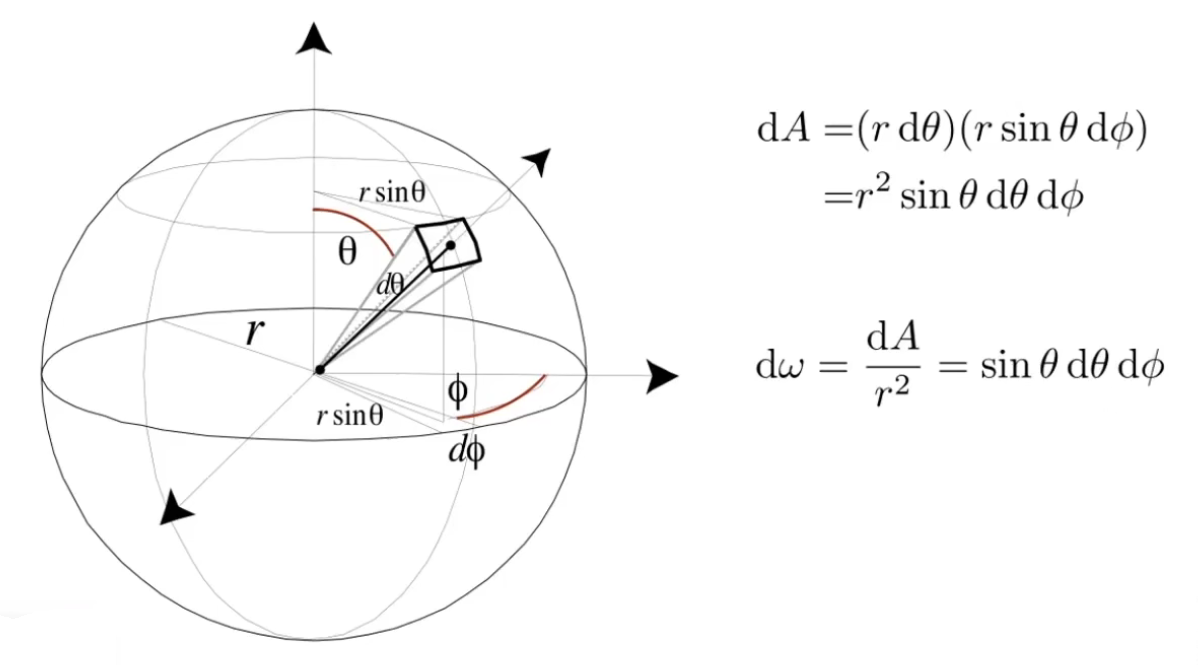
立体角:Ω=r2A (sr)、单位立体角:dω=sinθdθdφ
一个完整球面的立体角是 4π。
Irradiance
- E(x)=dAdΦ(x) (m2W)
辐射照度,功率每垂直面积。
Radiance
- L(p,ω)=dωdAcosθd2Φ(p,ω) (sr⋅m2W)
辐射亮度,功率每立体角,每垂直面积。可以理解为单位面积对单位立体角辐射或接受的功率。
推导
由定义可得 Radiance 即 Intensity 每垂直面积,或者 Irradiance 每立体角。
它们之间的转换为:
- dE(p)=L(p,ω)∗cosθdω
- dI(p,ω)=L(p,ω)∗cosθdA
进一步推导:一单位面积的 Irradiance 为其接受的 Radiance 在单位半球上的积分。
- E(p)=∫H2Li(p,ω)cosθdω
双向反射分布函数 BRDF
该函数定义了某一单位面积从某一单位立体角接收到的 Radiance 转化为其 Irradiance 然后再辐射出去的 Radiance 是如何分配到各个立体角上的,即:
出射 Radiance / 入射 Irradiance
- fr(ωi→ωr)=dEiωidLrωr=Li(p,ωi)cosθidωidLr(ωr) (sr1)
反射方程
由 Radiance 与 BRDF 的定义可得:单位面积向任一单位立体角辐射出的 Radiance 可由其接受的 Radiance 与其 BRDF 的乘积在单位半球上积分求得。
- Lr(p,ωr)=∫H2fr(p,ωi→ωr)Li(p,ωi)cosθidωi
渲染方程
在反射方程中加上自发光项,用于描述光源物体。
- Lo(p,ωo)=Le(p,ωo)+∫H2fr(p,ωi,ωo)Li(p,ωi)(n⋅ωi)dωi
H2 和 Ω+ 都表示单位半球面,我们默认下半球面不会产生任何贡献,这样就不用写什么 max(0,cosθ) 了。
