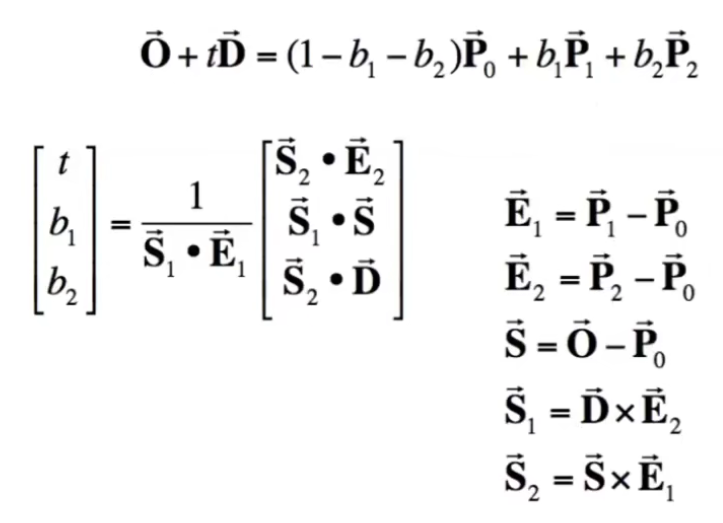【Archive】GAMES101

渲染管线中的变换矩阵

在渲染管线的前期，光栅化之前，需要对顶点和相机的坐标进行标准化变换，然后进行视口变换进入屏幕坐标空间。

相机的定义

位置： $\vec{e}$ ; 看向： $\vec{g}$ ; 上方： $\vec{t}$ ;

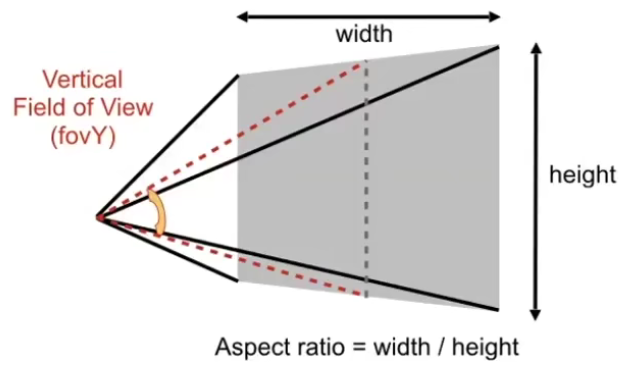
我们规定相机位于 (0, 0, 0) ，看向 -Z，上方为 Y。
对相机和顶点应用同一个变换矩阵，他们的相对位置则不变。

视锥体的定义

已知fovY和aspect可得

$tan\frac{fovY}{2} = \frac{t}{|n|}$
$aspect = \frac{r}{t}$

像素空间

像素块编号 (0, 0) -> (width - 1, height - 1)
像素中心 (x + 0.5, y + 0.5)
覆盖于 (0, 0) -> (width, height)

Viewing

Model-View

$M_{view}=R_{view}T_{view}$

将相机移动至原点。
$T_{view}=$

\begin{pmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

然后将 g 旋转至 -Z，t 旋转至 Y，（g x t）旋转至 X。
但是这样的矩阵不好求，故先考虑求其简单的逆矩阵 $R_{view}^{-1}$ ：

将 X（1，0，0）旋转至（g x t），将 Y（0，1，0）旋转至 t，将 Z（0，0，1）旋转至 -g。
同时，旋转矩阵是正交矩阵，故其逆矩阵等于其转置矩阵。

由 $R_{view}^{-1}=$

\begin{pmatrix} x_{g \times t} & x_t & x_{-g} & 0 \\ y_{g \times t} & y_t & y_{-g} & 0 \\ z_{g \times t} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

得 $R_{view}=$

\begin{pmatrix} x_{g \times t} & y_{g \times t} & z_{g \times t} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Projection

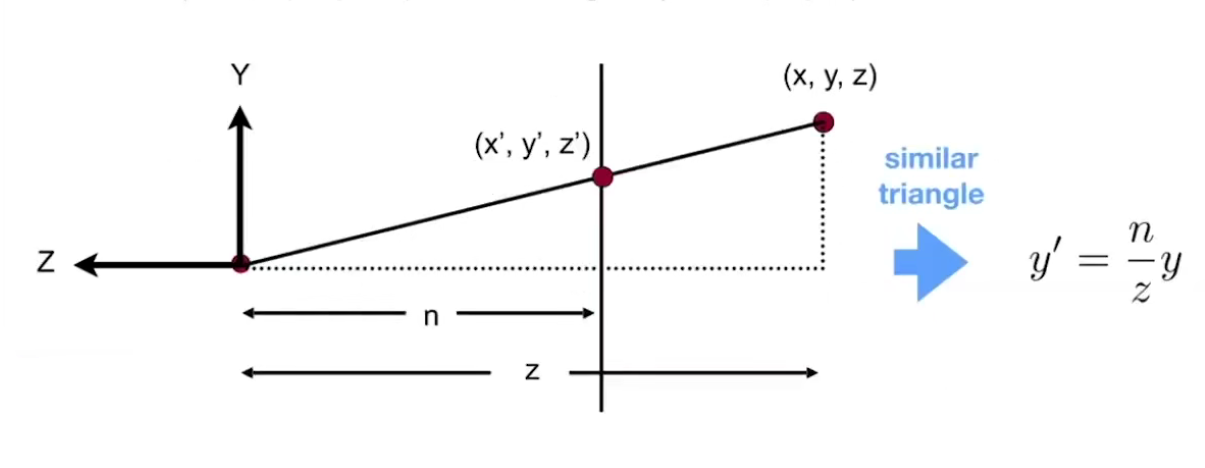
Persprctive to Orthographic

得 $y^, = \frac{n}{z}y$ ; $x^, = \frac{n}{z}x$ ;

在齐次坐标系下，对一个坐标的所有元素乘以或除以同一个数仍然代表原本的坐标。

故一点 $(x,y,z,1)^T$ 乘 $M_{p2o}$ 之后会被变换至：

\begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ ? \\ 1 \\ \end{pmatrix}

即：

\begin{pmatrix} nx \\ ny \\ ? \\ z \\ \end{pmatrix}

所以：
$M_{p2o} =$

\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}

又因为 f、n 平面在变换后 z 轴不变，
即近平面上一点 $(x,y,n,1)^T$ 乘 $(?,?,?,?)$ 得 n，或者说，得 $n^2$ 。
得：

$(?,?,?,?)=(0,0,A,B)$ 且 $An+B=n^2$

且远平面上中心点 $(0,0,f,1)^T$ 乘 $(0,0,A,B)$ 得 f，或者说，得 $f^2$ 。
得：

$Af+B=f^2$

联立得：

$(0,0,A,B)=(0,0,n+f,-nf)$

综上所述， $M_{p2o}=$

\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}

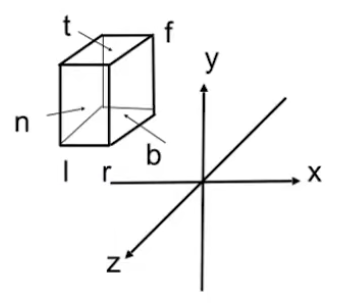
Orthographic

将裁剪空间转化为标准化设备坐标，中心为 (0, 0, 0)，大小为 1x1x1 的立方体。

注意这里 l<r b<t f>n。

$M_{ortho}=$

\begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{2} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{2} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Projection

$M_{Projection}=M_{Orthographic}M_{PersprctiveToOrthographic}$

Viewport

先将标准化设备坐标拉伸至与屏幕同等大小，再将其中心(0, 0)移至屏幕中心。保留z轴不变用于之后做深度检测。
$M_{viewport}=$

\begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}

Super Sample Anti-Aliasing

SSAA 作为一种暴力的超采样手段带来的性能开销是难以接受的，但作为反走样的入门仍然有学习一下的必要。

insideTriangle

判断两向量的左右关系

假设两向量 $\vec{a}$ 、 $\vec{b}$ 在同一 z 轴为 0 的平面上，根据右手螺旋定则，若 $\vec{a} \times \vec{b}$ 的 z 轴大于 0 则 $\vec{b}$ 在 $\vec{a}$ 的左侧，反之亦然。

那么对于三角形三点形成的顺\逆时针三条向量来说，若有一点同时位于三向量的同一侧，则该点位于三角形内部。

假设三角形三点 a、b、c 与点 p 在同一平面上。
三角形三点按顺序形成三条向量 $\vec{ab}$ 、 $\vec{bc}$ 、 $\vec{ca}$ ，与 p 点形成三向条量 $\vec{ap}$ 、 $\vec{bp}$ 、 $\vec{cp}$ 。
将他们分别叉乘，判断结果是否同号即可判断三角形是否包围点。

static bool insideTriangle(float x, float y, const Vector3f* _v) {
	Eigen::Vector3f p(x, y, 0);
	Eigen::Vector3f a(_v[0][0], _v[0][1], 0);
	Eigen::Vector3f b(_v[1][0], _v[1][1], 0);
	Eigen::Vector3f c(_v[2][0], _v[2][1], 0);

	Eigen::Vector3f ab = b - a;
	Eigen::Vector3f bc = c - b;
	Eigen::Vector3f ca = a - c;

	Eigen::Vector3f ap = p - a;
	Eigen::Vector3f bp = p - b;
	Eigen::Vector3f cp = p - c;

	Eigen::Vector3f crs1 = ab.cross(ap);
	Eigen::Vector3f crs2 = bc.cross(bp);
	Eigen::Vector3f crs3 = ca.cross(cp);

	return ((crs1[2] >= 0 && crs2[2] >= 0 && crs3[2] >= 0) ||
		(crs1[2] <= 0 && crs2[2] <= 0 && crs3[2] <= 0));
}

SSAA & zBuffer

遍历包围盒内的像素，对于每个像素遍历每个超采样点，确定三角形覆盖像素的比例，通过重心坐标计算对应的深度值，与深度缓存做比较并写入帧缓存。

void rst::rasterizer::rasterize_triangle(const Triangle& t) {
	auto v = t.toVector4();

	// 包围盒大小
	int minX = (int)std::floor(std::min(v[0][0], std::min(v[1][0], v[2][0])));
	int maxX = (int)std::ceil(std::max(v[0][0], std::max(v[1][0], v[2][0])));
	int minY = (int)std::floor(std::min(v[0][1], std::min(v[1][1], v[2][1])));
	int maxY = (int)std::ceil(std::max(v[0][1], std::max(v[1][1], v[2][1])));

	// 四个超采样点的相对坐标
	std::vector<Eigen::Vector2f> super{
		{0.25f,0.25f},
		{0.75f,0.25f},
		{0.25f,0.75f},
		{0.75f,0.75f},
	};

	// 遍历包围盒内所有像素点
	for (int x = minX; x <= maxX; x++) {
		for (int y = minY; y <= maxY; y++) {
			int insideCount = 0;
			float sumDepth = 0.f;

			// 遍历像素点内所有超采样点
			for (int i = 0; i < 4; i++) {
				if (insideTriangle((float)x + super[i][0],
					(float)y + super[i][1], t.v)) {
					insideCount++;

					// 计算重心坐标
					auto tup = computeBarycentric2D(
						(float)x + super[i][0], (float)y + super[i][1], t.v);

					float alpha, beta, gamma;
					std::tie(alpha, beta, gamma) = tup;

					// 利用重心坐标计算深度插值
					float w_reciprocal = 1.f /
						(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
					float z_interpolated = alpha * v[0].z() / v[0].w() +
						beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();

					z_interpolated *= w_reciprocal;
					sumDepth += z_interpolated;
				}
			}
			if (insideCount > 0) {
				float avgDepth = sumDepth / 4.f;
				if (avgDepth < depth_buf[get_index(x, y)]) {
					depth_buf[get_index(x, y)] = avgDepth;

					Eigen::Vector3f point((float)x, (float)y, avgDepth);
					Eigen::Vector3f color = t.getColor() * insideCount / 4.f;
					set_pixel(point, color);
				}
			}
		}
	}
}

结果

Blinn-Phong 光照模型

该模型将任一点的光照分为三部分：1.由光源方向与法线方向决定的漫反射、2.由光源方向法线方向与观察方向决定的高光、3.恒定的环境光。

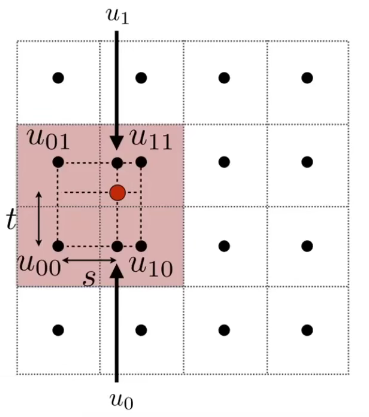
getColorBilinear

对贴图采样时采用双线性插值的方法以获得柔和的过度。

Eigen::Vector3f getColorBilinear(float u, float v) {
	if (u > 1) u = u - (int)u;
	if (u < 0) u = u - (int)u + 1;
	if (v > 1) v = v - (int)v;
	if (v < 0) v = v - (int)v + 1;

	float u_img = u * width;
	float v_img = (1 - v) * height;

	int u_min = (int)std::floor(u_img);
	int u_max = (int)std::min((float)width, std::ceil(u_img));
	int v_min = (int)std::floor(v_img);
	int v_max = (int)std::min((float)height, std::ceil(v_img));

	auto u00 = image_data.at<cv::Vec3b>(v_min, u_min);
	auto u01 = image_data.at<cv::Vec3b>(v_max, u_min);
	auto u10 = image_data.at<cv::Vec3b>(v_min, u_max);
	auto u11 = image_data.at<cv::Vec3b>(v_max, u_max);

	float s = (u_img - u_min) / (u_max - u_min);
	float t = (v_img - v_min) / (v_max - v_min);

	auto u0 = (1 - s) * u00 + s * u10;
	auto u1 = (1 - s) * u01 + s * u11;
	auto p = (1 - t) * u0 + t * u1;

	return Eigen::Vector3f(p[0], p[1], p[2]);
}

布林-冯

公式中的 k 代表材质对光的反射强度，当分别处理 k 中 RBG 三通道时即可表示不同颜色，当将读取到的贴图颜色应用于 k 时即可显示贴图。
高光公式中的 p 代表高光的集中程度，由于 cos 函数趋向 0 的速度过慢，因此使用 cos 的 p 次方使高光更加集中。p 的值也可以存在一张贴图中。
I / r2 用于模拟光线的衰减。

Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload) {
	Eigen::Vector3f texture_color = Eigen::Vector3f::Identity();
	bool isBilinear = true;
	if (payload.texture) {
		if (isBilinear) {
			texture_color = payload.texture->getColorBilinear(
				payload.tex_coords.x(), payload.tex_coords.y());
		}
		else {
			texture_color = payload.texture->getColor(
				payload.tex_coords.x(), payload.tex_coords.y());
		}
	}

	// 反射系数
	Eigen::Vector3f kd = texture_color / 255.f;
	Eigen::Vector3f ks = Eigen::Vector3f(0.7937f, 0.7937f, 0.7937f);
	Eigen::Vector3f ka = Eigen::Vector3f(0.01f, 0.01f, 0.01f);

	// 光源
	auto l1 = light{ {20, 20, 20}, {500, 500, 500} };
	auto l2 = light{ {-20, 20, 0}, {500, 500, 500} };

	float p = 200.0f;// 幂系数
	std::vector<light> lights = { l1, l2 };// 打包光源
	Eigen::Vector3f amb_light_intensity{ 10, 10, 10 };// 环境光强度
	Eigen::Vector3f eye_pos{ 0, 0, 10 };// 相机位置

	// 用于计算的向量
	Eigen::Vector3f point = payload.view_pos;
	Eigen::Vector3f normal = payload.normal;
	Eigen::Vector3f viewVector = eye_pos - point;

	Eigen::Vector3f result_color = { 0, 0, 0 };
	for (auto& light : lights) {
		Eigen::Vector3f lightVector = light.position - point;
		float r2 = lightVector.dot(lightVector);

		// 漫反射
		Eigen::Vector3f ld = kd.cwiseProduct(light.intensity) / r2 *
			std::max(0.f, normal.dot(lightVector.normalized()));
		result_color += ld;
		
		// 高光
		Eigen::Vector3f vpl = viewVector.normalized() + lightVector.normalized();
		Eigen::Vector3f h = vpl / vpl.norm();//半程向量
		Eigen::Vector3f ls = ks.cwiseProduct(light.intensity) / r2 *
			pow(std::max(0.f, normal.dot(h)), p);
		result_color += ls;
	}
	// 环境光
	Eigen::Vector3f la = ka.cwiseProduct(amb_light_intensity);
	result_color += la;

	return result_color * 255.f;
}

结果

Whitted-Style 光线追踪

Whitted_Style 光线追踪的部分实现，包括射线与由重心坐标表式的三角形相交、射线与轴对齐包围盒的相交、包围盒的树形加速结构。

Möller-Trumbore 射线与平面（重心坐标）

光线的定义：

$\vec{O}+t\vec{D}$

平面的定义：

$(1-b_1-b_2)\vec{P}_0+b_1\vec{P}_1+b_2\vec{P}_2$

求射线与平面的交点即联立两表达式求解，已知 xyz 三分量上的三对表达式，求未知量：t、 $b_1$ 、 $b_2$ 。

对于用重心坐标表示的三角形，三值之和为 1 即可表示当前平面上的任一点，若同时三值均大于 1 则表示该三角形内部的一点。

bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2,
	const Vector3f& orig, const Vector3f& dir) {

	Vector3f e1 = v1 - v0;
	Vector3f e2 = v2 - v0;
	Vector3f s = orig - v0;
	Vector3f s1 = crossProduct(dir, e2);
	Vector3f s2 = crossProduct(s, e1);

	float factor = dotProduct(s1, e1);
	float t = dotProduct(s2, e2) / factor;
	float b1 = dotProduct(s1, s) / factor;
	float b2 = dotProduct(s2, dir) / factor;

	if (t >= 0 && b1 >= 0 && b2 >= 0 && (1 - b1 - b2) >= 0)
		return true;
	return false;
}

射线与平面（点法式）

平面的定义：

$(\vec{P}-\vec{P^,})\cdot \vec{N}$

点 $P^,$ 与法向量 N 组成一平面，P 为面上任一点。
将射线代入 P 得

$t=\frac{(\vec{P^,}-\vec{O})\cdot \vec{N}}{\vec{D}\cdot \vec{N}}$

射线与轴对齐包围盒

包围盒的定义：pMax 与 pMin 两个点所代表的三对面。
射线与轴对齐平面的相交（例如x轴）：

$t=\frac{\vec{P^,_x}-\vec{O_x}}{\vec{D_x}}$

对于每一对平面，射线存在一对与他们相交的 $t_{min}$ 与 $t_{max}$
射线进入包围盒：射线进入所有三对面；射线离开包围盒：射线离开任一面。

$t_{enter}=max(t_{min})$ 、 $t_{exit}=min(t_{max})$

射线与包围盒有一段相交： $t_{enter}<t_{exit}$

#include <limits>
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
	const std::array<bool, 3>& dirIsNeg) const {

	/* invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z),
	   use this because Multiply is faster that Division */
	/* dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)],
	   use this to simplify your logic */

	float tEnter = std::numeric_limits<float>::lowest();
	float tExit = std::numeric_limits<float>::max();
	for (int i = 0; i < 3; i++) {
		float tMin = (pMin[i] - ray.origin[i]) * invDir[i];
		float tMax = (pMax[i] - ray.origin[i]) * invDir[i];
		/* 如果光线沿负方向传播，光线会先撞上pMax的对应的维度得到tMax，
		   而此t应是光线进入包围盒时的tMin。出包围盒时同理。*/
		if (dirIsNeg[i]) {
			std::swap(tMin, tMax);
		}
		if (tMin > tEnter) {
			tEnter = tMin;
		}
		if (tMax < tExit) {
			tExit = tMax;
		}
	}
	return (tEnter < tExit && tExit >= 0);
}

BVH 的创建

轴对齐包围盒的加速结构

BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects) {
	BVHBuildNode* node = new BVHBuildNode();

	Bounds3 bounds;
	for (int i = 0; i < objects.size(); ++i)
		bounds = Union(bounds, objects[i]->getBounds());
	if (objects.size() == 1) {
		// 创建叶节点
		node->bounds = objects[0]->getBounds();
		node->object = objects[0];
		node->left = nullptr;
		node->right = nullptr;
		return node;
	}
	else if (objects.size() == 2) {
		node->left = recursiveBuild(std::vector{objects[0]});
		node->right = recursiveBuild(std::vector{objects[1]});

		node->bounds = Union(node->left->bounds, node->right->bounds);
		return node;
	}
	else {
		Bounds3 centroidBounds;
		for (int i = 0; i < objects.size(); ++i)
			centroidBounds = Union(centroidBounds, objects[i]->getBounds().Centroid());
		// 返回包围盒大致的形状以决定接下来以哪个轴分割包围盒
		int dim = centroidBounds.maxExtent();
		switch (dim) {
			case 0:
				std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
					return f1->getBounds().Centroid().x <
						f2->getBounds().Centroid().x;
				});
				break;
			case 1:
				std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
					return f1->getBounds().Centroid().y <
						f2->getBounds().Centroid().y;
				});
				break;
			case 2:
				std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
					return f1->getBounds().Centroid().z <
						f2->getBounds().Centroid().z;
				});
				break;
		}

		auto beginning = objects.begin();
		auto middling = objects.begin() + (objects.size() / 2);
		auto ending = objects.end();

		auto leftshapes = std::vector<Object*>(beginning, middling);
		auto rightshapes = std::vector<Object*>(middling, ending);

		assert(objects.size() == (leftshapes.size() + rightshapes.size()));

		node->left = recursiveBuild(leftshapes);
		node->right = recursiveBuild(rightshapes);

		node->bounds = Union(node->left->bounds, node->right->bounds);
	}

	return node;
}

BVH 的创建（ASH）

表面积启发式算法基于两个假设：如果包围盒的表面积越大，那么它被射线击中的可能性也就越大。包围盒内的物体数量越多，遍历它的开销就越大。比较所有划分方案的预计开销并选择最优的方案。
开销：float cost = 1 + (countA * A.SurfaceArea() + countB * B.SurfaceArea()) / nArea;

BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects) {
	BVHBuildNode* node = new BVHBuildNode();

	Bounds3 bounds;
	for (int i = 0; i < objects.size(); ++i) {
		bounds = Union(bounds, objects[i]->getBounds());
	}
	if (objects.size() == 1) {
		// 创建叶节点
		node->bounds = objects[0]->getBounds();
		node->object = objects[0];
		node->left = nullptr;
		node->right = nullptr;
		return node;
	}
	else if (objects.size() == 2) {
		node->left = recursiveBuild(std::vector{objects[0]});
		node->right = recursiveBuild(std::vector{objects[1]});

		node->bounds = Union(node->left->bounds, node->right->bounds);
		return node;
	}
	else {
		Bounds3 centroidBounds;
		for (int i = 0; i < objects.size(); ++i) {
			centroidBounds = Union(centroidBounds,objects[i]->getBounds().Centroid());
		}
		std::vector<Object*> leftshapes;
		std::vector<Object*> rightshapes;

		Bounds3 nBounds;
		for (int i = 0; i < objects.size(); ++i) {
			nBounds = Union(nBounds, objects[i]->getBounds());
		}
		float nArea = centroidBounds.SurfaceArea();

		int minCostCoor = 0;
		int mincostIndex = 0;
		float minCost = std::numeric_limits<float>::infinity();
		std::map<int, std::map<int, int>> indexMap;
		for (int i = 0; i < 3; i++) {
			int bucketCount = 12;
			std::vector<Bounds3> boundsBuckets;
			std::vector<int> countBucket;
			for (int j = 0; j < bucketCount; j++) {
				boundsBuckets.push_back(Bounds3());
				countBucket.push_back(0);
			}

			std::map<int, int> objMap;

			for (int j = 0; j < objects.size(); j++) {
				int bid = bucketCount * centroidBounds.Offset(
					objects[j]->getBounds().Centroid())[i];

				if (bid > bucketCount - 1) {
					bid = bucketCount - 1;
				}
				Bounds3 b = boundsBuckets[bid];
				b = Union(b, objects[j]->getBounds().Centroid());
				boundsBuckets[bid] = b;
				countBucket[bid] = countBucket[bid] + 1;
				objMap.insert(std::make_pair(j, bid));
			}

			indexMap.insert(std::make_pair(i, objMap));

			for (int j = 1; j < boundsBuckets.size(); j++) {
				Bounds3 A;
				Bounds3 B;
				int countA = 0;
				int countB = 0;
				for (int k = 0; k < j; k++) {
					A = Union(A, boundsBuckets[k]);
					countA += countBucket[k];
				}

				for (int k = j; k < boundsBuckets.size(); k++) {
					B = Union(B, boundsBuckets[k]);
					countB += countBucket[k];
				}

				float cost = 1 + (countA * A.SurfaceArea() +
					countB * B.SurfaceArea()) / nArea;

				if (cost < minCost) {
					minCost = cost;
					mincostIndex = j;
					minCostCoor = i;
				}
			}
		}

		for (int i = 0; i < objects.size(); i++) {
			if (indexMap[minCostCoor][i] < mincostIndex) {
				leftshapes.push_back(objects[i]);
			}
			else {
				rightshapes.push_back(objects[i]);
			}
		}
	
		assert(objects.size() == (leftshapes.size() + rightshapes.size()));

		node->left = recursiveBuild(leftshapes);
		node->right = recursiveBuild(rightshapes);

		node->bounds = Union(node->left->bounds, node->right->bounds);
	}

	return node;
}

BVH 的遍历

Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const {
	Intersection inter;

	float x = ray.direction.x;
	float y = ray.direction.y;
	float z = ray.direction.z;
	std::array<bool, 3> dirsIsNeg{x < 0,y < 0,z < 0};
	// 与此节点的包围盒不相交
	if (node->bounds.IntersectP(ray, ray.direction_inv, dirsIsNeg) == false) {
		return inter;
	}
	// 遍历到叶节点
	if (node->left == nullptr && node->right == nullptr)     {
		inter = node->object->getIntersection(ray);
		return inter;
	}
	Intersection hitL = getIntersection(node->left, ray);
	Intersection hitR = getIntersection(node->right, ray);

	if (hitL.distance < hitR.distance) {
		return hitL;
	}

	return hitR;
}

结果

蒙特卡洛路径追踪

我们在上一章中得到了重要的渲染方程，在这一章中将使用蒙特卡洛算法实现方程中的积分，并用俄罗斯轮盘赌实现间接光照中对渲染方程的递归调用。

蒙特卡洛

按一定分布对原函数进行随机采样，利用概率分布函数进行加权平均。

$\int f(x){\rm d}x=\frac{1}{N}\sum^{N}_{i=1}\frac{f(X_i)}{p^,(X_i)}$ $X_i$ ~ $p^,(x)$
$L_o(p,\omega_o)\approx \frac{1}{N}\sum^{N}_{i=1}\frac{L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot \omega_i)}{p^,(\omega_i)}$

将定积分求解转化为对随机变量求平均。
当我们对半球进行均匀采样时： $p^,(\omega_i)=\frac{\pi}{2}$

路径追踪

若计算每根光线反射出的N跟光线，递归次数呈指数级上涨，开销难以接受。
解决方法：对一个像素内多次发射出一根光线，每次反射只产生一根光线，结果求平均。此时上方的N = 1。

俄罗斯轮盘赌

接下来解决递归如何返回的问题。在真实世界中的光线可能会经过无数次弹射才进入人眼，但在有限的计算时间内这几乎是无法模拟的。
解决方法：以期望代替无限次递归逼近的结果。设一小数 p(0,1)，每次递归内以概率 (p - 1) 直接返回 0，以概率 p 进入下一层递归，并对结果除以 p。此时递归的期望为：

$E=P*(L_o/P)+(1-P)*0=L_o$

递归的期望值确实是正确的，但是根据实现的不同，或者受制于显示器色域，超过 255 的值可能被截断至 255，导致结果看起来偏暗。

最后一个问题

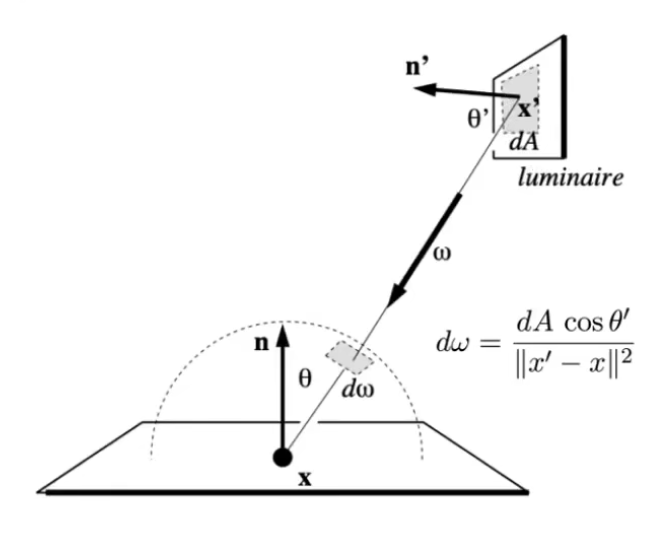
在目前的算法中，从视点发射出的一根光线若直到最终都没有击中发光物体便不会返回任何 Radiance。这样在场景中光源表面积非常小的情况下便很难产生有效的递归，因为对半球内方向随机采样难以精确采样到发光物体。
解决方法：每层递归内将直接光照与间接光照的贡献分离开，并直接对光源进行采样。这时需要将光源方向 $\omega$ 转换为光源在单位球面上对应的面积 A，然后对 A 做积分，此时的概率密度函数为 $\frac{1}{A}$

$d\omega=\frac{\cos \theta^,dA}{|x^,-x|^2}$

可以理解为 $\cos \theta^,$ 负责把光源的面积转过来做为一个锥体的底部，再根据相似三角形原理将面积缩放到单位球面上。
光源对单位面积的贡献为：

$L_o(x,\omega_o)=\int_ALi(x,\omega_i)f_r(x,\omega_i,\omega_o)\frac{\cos \theta \cos \theta^,}{|x^,-x|^2}{\rm d}A$

伪代码

Shad(p, wo) {
对光源采样（pdf_light = 1 / A）
if (p点与光源间无遮挡)
L_dir = Li * f_r * cos $\theta$ * cos $\theta^,$ / $|x^,-p|^2$ / pdf_light
俄罗斯轮盘赌 P_RR
对半球采样（pdf_hemi = 1 / 2 $\pi$ ）
追踪光线 r(p, wi)
if (r 击中非发光物体 q)
L_indir = Shad(q, -wi) * f_r * $\cos \theta$ / pdf_hemi / P_RR
return L_dir + L_indir
}

代码实现

Vector3f Scene::castRay(const Ray& ray, int depth) const {
	Intersection inter = intersect(ray);

	if (inter.happened) {
		if (inter.m->hasEmission()) {
			// 如果视线可以直接捕捉光源
			if (depth == 0) {
				return inter.m->getEmission();
			}
			/* 任何 Secondary Ray 击中光源时不返回亮度，
			   光源提供的亮度由每个非光源交点对光源采样得到 */
			else {
				return Vector3f(0, 0, 0);
			}
		}

		Vector3f L_dir(0, 0, 0);
		Vector3f L_indir(0, 0, 0);

		Intersection lightInter;
		float pdf_light = 0.f;
		sampleLight(lightInter, pdf_light);

		// 物体表面单位法向量
		Vector3f N = inter.normal;
		// 光源表面单位法向量
		Vector3f NN = lightInter.normal;

		Vector3f objPos = inter.coords;
		Vector3f lightPos = lightInter.coords;

		Vector3f objectToLight = lightPos - objPos;
		// objectToLightDierction
		Vector3f o2lDir = objectToLight.normalized();
		// objectToLightIntersection
		Intersection o2lInter = intersect(Ray(objPos, o2lDir));

		// 如果反射击中光源
		if (o2lInter.happened && o2lInter.m->hasEmission()) {
			// (o2lInter.coords - lightPos).norm() < 1e-2
			Vector3f f_r = inter.m->eval(ray.direction, o2lDir, N);
			L_dir = lightInter.emit * f_r *
				dotProduct(o2lDir, N) * dotProduct(-o2lDir, NN) /
				dotProduct(objectToLight, objectToLight) / pdf_light;
		}

		if (get_random_float() > RussianRoulette) {
			return Vector3f(0, 0, 0);
		}

		Vector3f nextDir = inter.m->sample(ray.direction, N).normalized();
		Ray nextRay(objPos, nextDir);
		Intersection nextInter = intersect(nextRay);
		if (nextInter.happened && !nextInter.m->hasEmission()) {
			float pdf_hemi = inter.m->pdf(ray.direction, nextDir, N);
			Vector3f f_r = inter.m->eval(ray.direction, nextDir, N);
			L_indir = castRay(nextRay, depth + 1) * f_r * dotProduct(nextDir, N) /
				pdf_hemi / RussianRoulette;
		}

		return L_dir + L_indir;
	}

	return Vector3f(0, 0, 0);
}

结果

微表面模型

所有的 PBR 技术都基于微表面理论。这项理论认为，达到微观尺度之后任何表面都可以用被称为微表面 (Microfacets) 的细小镜面来进行描绘。在微观尺度下，没有任何表面是完全光滑的。然而由于这些微表面已经微小到无法逐像素的继续对其进行区分，因此我们只有假设一个粗糙度 (Roughness) 参数，然后用统计学的方法来概略的估算微表面的粗糙程度。

BRDF

性质
非负、线性、可逆、能量守恒、各向同性、各向异性

$f(i,o)=\frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)}$

F：菲涅尔方程，定义不同表面角下，表面所反射光线占比。
D：法线的分布。
G：当 i 或 o 几乎平行于表面时，微观下凹凸不平的表面会发生自遮挡。

代码实现

这里参考 LearnOpenGL 给出的实现。
并且只考虑 PBR 材质中的金属度与粗糙度。

从下往上球体的金属性从0.0变到1.0，从左到右球体的粗糙度从0.0变到1.0。

菲涅尔方程的近似

这里在 0.04 - ALBEDO (0.96) 间用金属度做插值，0.04 为基础反射率，0.96 接近于铝的反射率。
可以简单地认为导体的反射率大于绝缘体，并且对于导体表面，使用它们的折射指数计算基础折射率并不能得出正确的结果。所以我们预先计算出平面的反射率，然后基于相应观察角的 Fresnel-Schlick 近似对这个值进行插值，这样我们就能对金属和非金属材质使用同一个公式了。

#define ALBEDO 0.96f

float FresnelSchlick(const Vector3f& H, const Vector3f& V, const float& metalness) const {
    float inter = 0.04f * (1 - metalness) + ALBEDO * metalness;
    float cosTheta = std::max(dotProduct(H, V), 0.f);

    return inter + (1.f - inter) * pow(1.f - cosTheta, 5.f);
}

法线分布模型

// 表示法线分布方向的正态分布函数
float DistributionGGX(Vector3f N, Vector3f H, float roughness) {
    float a = roughness * roughness;
    float a2 = a * a;
    float NdotH = std::max(dotProduct(N, H), 0.f);
    float NdotH2 = NdotH * NdotH;

    float nom = a2;
    float denom = (NdotH2 * (a2 - 1.f) + 1.f);
    denom = M_PI * denom * denom;

    return nom / std::max(denom, 1e-5f);
}

几何函数

float GeometrySchlickGGX(float NdotV, float roughness) {
    float r = (roughness + 1.f);
    float k = (r * r) / 8.f;

    float nom = NdotV;
    float denom = NdotV * (1.f - k) + k;

    return nom / std::max(denom, 1e-5f);
}
// 从统计学上近似的求得微平面间相互遮蔽的比率
float GeometrySmith(Vector3f N, Vector3f V, Vector3f L, float roughness) {
    float NdotV = std::max(dotProduct(N, V), 0.f);
    float NdotL = std::max(dotProduct(N, L), 0.f);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

BRDF

#define ALBEDO 0.96f

Vector3f Material::eval(const Vector3f &wi, const Vector3f &wo, const Vector3f &N){
    switch(m_type){
        case DIFFUSE:
        {
            float cosalpha = dotProduct(N, wo);
            if (cosalpha > 0.f) {
                Vector3f diffuse = Kd / M_PI;
                return diffuse;
            }
            else
                return Vector3f(0.f);
            break;
        }
        case Microfacet:
        {
            float cosalpha = dotProduct(N, wo);
            if (cosalpha > 0.f) {
                float roughness = 0.9f;
                float metallic = 0.9f;

                Vector3f V = -wi;
                Vector3f L = wo;
                Vector3f H = normalize(V + L);

                float F = Material::FresnelSchlick(H, V, metallic);
                float G = Material::GeometrySmith(N, V, L, roughness);
                float D = Material::DistributionGGX(N, H, roughness);

                Vector3f nominator = F * G * D;
                float denominator = 4 * std::max(dotProduct(N, V), 0.f) * 
                    std::max(dotProduct(N, L), 0.f);
                Vector3f specular = nominator / std::max(denominator, 1e-5f);
                
                Vector3f kS = F;
                Vector3f kD = Vector3f(1.f) - kS;
                kD = kD * Vector3f(1.f - metallic);

                Vector3f diffuse = ALBEDO / M_PI;

                /* 应当注意：这里的实现（微表面结合 diffuse）是 LearnOpenGL 提供的模型，
                   但是闫老师在 GAMES202 中指出这是错误且没有物理依据的。*/
                return kD * diffuse + specular;
            }
            else

                return Vector3f(0.f);
            break;
        }
    }
}